This suite of standalone software is to predict mechanical, thermal, conductivity, filtration and separation etc. properties for variant polymer materials.
0 Download
The polySML-PSI software can be download from:
- Github
- Baidu Disk (Download Code:
ubxm)
1 Purpose
This model provides the prediction for three interaction parameters between polymer and solvent and the evaluation of the good/poor solvent for polymers.
2 Requirements
Windows operation systems, including win7/vista/win8/win10 64Bit, at least 800M RAM and 1.5G free disk space needed.
Note: Spaces and special characters are not permitted in the installation directory.
3 Usage
-
Input correct SMILES for polymer (trimer) end with * (SMILES can be queried from Pubchem https://pubchem.ncbi.nlm.nih.gov/ ).
-
Input correct SMILES for solvent.
-
Input testing temperature.
-
Check all the inputs correct and click Submit for predictions.
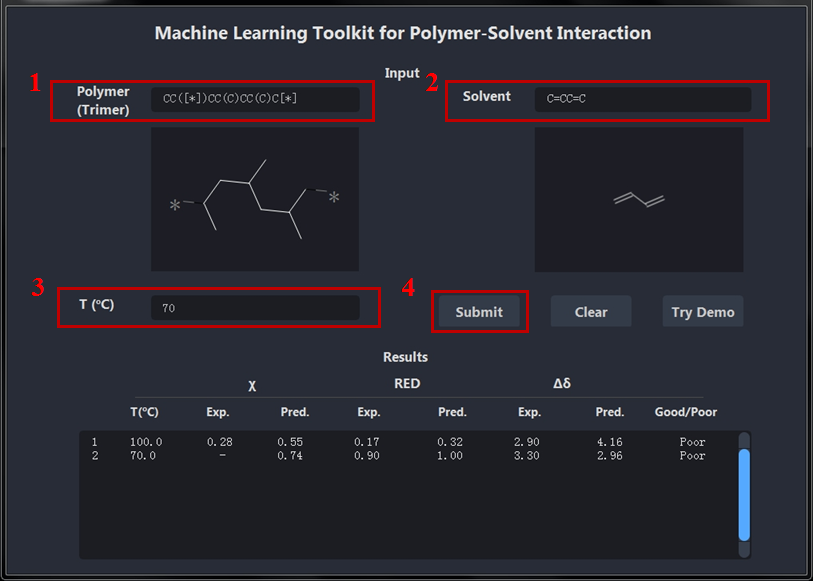
4 Predictor: polySML-PSI
4.1 Regression models
Flory-Huggins interaction parameter(χ)
The $χ$ is defined through the mixing free energy ($ΔG_{mix}$) for a polymer solution, written as:
$$ \frac{\Delta G_{mix}}{RT} = \frac{\phi_P}{N}ln \phi_P + (1 - ln \phi_P) ln (1- \phi_P) + \chi\phi_P(1-\phi_P) $$
Where $ϕ_P$ is the volume fraction of polymer, and $χ$ can be calculated by $χ = 0.5(ε_{PP}+ε_{SS}) - ε_{PS}$, with $ε_{PP}$, $ε_{SS}$, $ε_{PS}$ are the paired interactions for polymer-polymer, solvent-solvent and polymer-solvent, respectively.
Hildebrand solubility parameter(Δδ)
The Hildebrand solubility ($Δδ$) is derived from the difference for the square root of cohesive energy density ($e_{coh}$, MPa) between polymer and solvent:
$$ \Delta \delta =|\delta_S - \delta_P|=|e_{coh,S}^{1/2}- e_{coh,P}^{1/2}| $$
Hansen solubility parameter(RED)
The RED is the relative distance of Ra against the interaction radius ($R_0$) of polymer, defined as:
$$ RED=\frac{\sqrt{4(\delta D_P-\delta D_S)^2) + (\delta P_P-\delta P_S)^2) + (\delta H_P-\delta H_S)^2}}{R_0} $$
Here $δ_D$ for dispersion (van der Waals), $δ_P$ for polarity (dipole moment) and $δ_H$ for hydrogen bonding.
4.2 Classification models
According to the cutoff values ($χ=0.5$, $Δδ=2.0$ $MPa^{1/2} $, $RED$=1.0 ), we got classification models which can divide the solvent into good or poor. The output result is Y means that good compatibility for a pair of polymer and solvent, on the contrary, the result is N.
5 References
Users are encouraged to cite the following references for special predictors.
-
Liu T, Liu L, Cui F, Ding F, & Li Y Predict the performance of Polyvinylidene fluoride, ployethersulfone and polysulfone micro/ultra/nano-filtration membranes, 2020, J. Mater. Chem. A, 2020, 8,21862–21871.
-
Liu L, Chen W, Liu T, Kong X, Zheng J, & Li Y Rational design of hydrocarbon-based sulfonated copolymers for proton exchange membranes J. Mater. Chem. A, 2019 7:11847-11857.
-
Liu L, Chen W, & Li Y A Statistical Study of Proton Conduction in $Nafion^®$-based Composite Membranes: Prediction, Filler Selection and Fabrication Methods J. Membr. Sci., 2018 549:393-402.
-
Liu L, Chen W, & Li Y An overview of the proton conductivity of nafion membranes through a statistical analysis J. Membr. Sci., 2016 504:1-9.
6 Limitation
Current models mainly focus on the types of polymers and solvents reported. For novel materials, chemical structures, predictions are made based on knowledge, confidence needs validation in blind-test. We are not guarantee the prediction is fully accurate but guidelines are possible.
7 Bug report and suggestions
Please contact either lyliu@ciac.ac.cn or yunqi@ciac.ac.cn for bugs or suggestions.
8 About us
We are a research group dedicated in structure and machine learning study on polymer materials. We are welcoming suggestions and collaborations. Contact Prof. Yunqi Li for further information.

